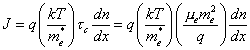Hall Effect

Basics of Hall Effect

In the Drude theory of the electrical conductivity of a metal, an electron is accelerated by the electric field for an average time , the relaxation or mean free time, before being scattered by impurities, lattice imperfections and phonons to a state which has average velocity zero. The average drift velocity of the electron is

where is the electric field and m is the electron mass. The current density is thus

where

and n is the electron density.

In the presence of a steady magnetic field, the conductivity and resistivity become tensors

and , . Still assuming that the relaxation time is , the Lorentz force must be added to the force from the electric field in Eq. (1),

In the steady state, . We will always assume that the magnetic field is in z direction . Then in xy plane

where is defined in Eq. (3),

is the cyclotron frequency. From Eq. (6), we can easily get

Eqs. (8) directly leads to the relation between conductivity and resistivity

We can see that if , the conductivity vanishes when the resistivity vanishes. On the other hand,

Therefore when , , where is given by the first term in Eq. (10), i.e. Hall conductivity

In the experiment we can let E=0,

The above discussion is the classical result. In quantum mechanics, the Hamiltonian is ( E is along x direction)

For this problem it is convenient to choose the Landau gauge, in which the vector potential is independent of y coordinate

This choice allows us to choose a wavefunction which has a plane-wave dependence on the y coordinate

Substituting Eq. (15) into Eq. (13), the Schrödinger equation becomes

where

is the classical cyclotron orbit radius.

Eq. (16) can be easily solved by transformation to a familiar harmonic oscillator equation. The eigenvalues and eigenstates are

where i=0,1,2,3, , and . The different oscillator levels are also called Landau Levels. The electric field simply shifts the eigenvalues by a value without changing the structure of the energy spectrum. From Figure 1 we can see that in two-dimensional systems, the Landau energy levels are completely seperate while in three-dimensional systems the spectrum is continuous due to the free movement of electrons in the direction of the magnetic field.

From the wave functions, we can calculate the mean value of the velocities

Thus =-neEc/B, which is the same as Eq. (11) of the classical result. The current along the direction of electric field (x) is zero at Landau levels.

Fig. 1 Schematic dagram of the density of states of two and three-dimensional electron systems

Semiconductor Transport: The Einstein Relations

The Einstein relations are important because they relate the diffusivity of a semiconductor to the mobility. Starting with the diffusion current (Diffusion, (4)).

(1)

From the theorem of equipartition of energy, which states that molecules in thermal equilibrium have the same average energy associated with each independent degree of freedom of their motion. In each of the three dimensions we have,

(2)

The expression for mobility is

(3)

Rearranging the equation (2) for the velocity, equation (3) for the mean free collision time, and substituting into equation (1) noting that the length is

(4)

Gives

(5)

A similar argument can be shown to give the Einstein relation for holes in the valence band.

Conductividad eléctrica

Una diferencia cuantitativa fundamental entre conductores, semiconductores y aislantes es la mayor o menor facilidad que presentan al paso de la corriente eléctrica, es decir, la conductividad que presentan los materiales.

En la tabla siguiente podemos observar el orden de magnitud de la conductividad para materiales aislantes, semiconductores y conductores.

Los semiconductores típicos puros, germanio y silicio, tienen conductividades que les situarían próximos a los aislantes. Pero si introducimos pequeñas cantidades, del orden de millonésimas partes, de otros elementos, su conductividad puede aumentar y situarse próxima a la de los conductores. A esta modificación de los semiconductores puros, se le denomina dopado, y se describirá con detalle más adelante.

Variación de la conductividad con la temperatura

En las gráficas de la figura podemos ver como para el cobre, al igual que todos los conductores, a temperaturas bajas la conductividad es grande, y disminuye al aumentar la temperatura, aunque manteniéndose en el mismo orden de magnitud. Sin embargo, en el germanio, como en todos los semiconductores puros, a temperaturas muy bajas la conductividad es prácticamente nula, y aumenta considerablemente al aumentar la temperatura.

Para el caso de semiconductores dopados se observa una variación de la conductividad con la temperatura diferente al caso de un semiconductor puro. En la gráfica de la Figura 8-4 se compara la conductividad del Si puro con la del Si dopado con dos concentraciones de impurezas diferentes. En el Si con impurezas se observa como a temperaturas muy bajas (próximas al cero absoluto) se produce un aumento brusco de la conductividad, después se mantiene constante, y aparece un nuevo aumento de la conductividad a temperaturas más altas análogo al caso del Si puro..

Variación de la conductividad con la iluminación del material

Cuando se ilumina un semiconductor con una radiación luminosa de energía variable se observa que la conductividad del material varía tal y como muestra la gráfica de la figura. En dicha gráfica observamos dos aspectos destacables:

1. Es necesario un valor mínimo de energía de los fotones para que la conductividad del material iluminado varíe, observando además en esa energía de los fotones un salto brusco en la conductividad.

2. Una variación en la energía de los fotones proporciona una variación en la conductividad del material.

Al realizar la misma experiencia con un material conductor, no se observa variación de la conductividad en función de la energía de los fotones.